Op 16-12-2019 om 19:00 uur precies start de première van de SPSS-clip over data cleaning. Oftewel: maak je data schoon voordat je start met analyseren.
Er is live video chat!
Boxplot
Deze student legt het nog een keer uit aan een andere student: ‘het is toch logisch dat het tweede kwartiel kleiner is dan de interkwartielafstand’.
De interkwartielafstand is bepaald door de ‘grijze box’ in de figuur, dat is het verschil tussen Q3 en Q1 en is óók een maat voor de spreiding.
Het tweede kwartiel is kleiner dan de interkwartielafstand? Nee, die vlieger gaat niet altijd op. Stel Q1=4, Q2=5 en Q3=6 .
Dan is de interkwartielafstand: Q3 – Q1 = 6 – 4 = 2.
Dus nee, want Q2=5 en is groter dan 2. (QED)
Histogram
Weifelend vraagt de student om bevestiging: ‘dus een histogram gebruik je alleen bij continue variabelen?’
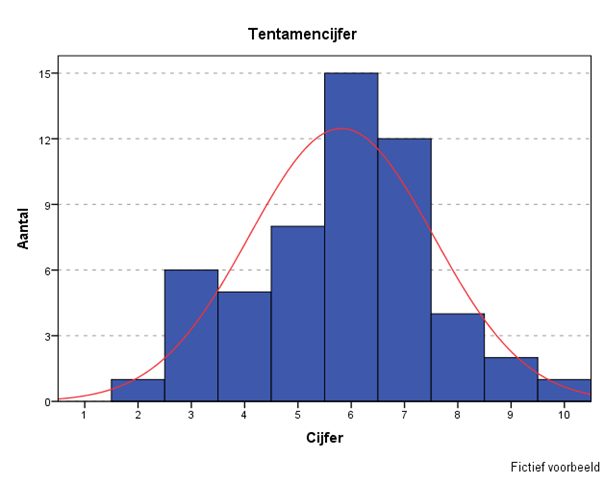
Ja!
Voor categorische variabelen, oftewel niet-continue variabelen, oftewel discrete variabelen gebruik je een (gewone) staafdiagram.
Chaos
Wat is de definitie van chaos?
Een statisticus zonder het toetstheorema van Fisher:
- Is er al een theoretische grondslag voor het verband?
- Welke richting kent het verband?
- Zijn de te onderzoeken variabelen onafhankelijk?
- Wat is de hypothese dat het verband formaliseert?
- Bepaal en bereken de toetsgrootheid.
- Conclusie: samenhang of niet?
Verzamelingen
Beter één verzameling in de hand, dan tien onbekend.
Statistiek is een doe-vak.
Steekproefgrootte in geval van interactie-effecten
Vraag van een student
Ik maak gebruik van 5 verschillende overtuigingsprincipes van Cialdini en één controlegroep. Dan klopt het toch dat ik na mijn steekproefberekening, die uitkwam op een minimum van 385 respondenten, in totaal (dus 5 principes + controlegroep) minimaal 385 respondenten moet hebben?
Antwoord
Van belang voor het antwoord is of er wel of geen interactie-effecten zijn. Laat ik het voorbeeld vertalen naar een nog wat eenvoudiger voorbeeld. Stel dat je wil weten wat de mensen van de kwaliteit van het brood van de bakker vinden, specifiek van:
- bruin brood;
- wit brood;
- stokbrood.
Opzet zonder interactie-effect
Dus je maakt een testopzet waarmee je een proefpanel organiseert die drie soorten brood gaan proeven. Je trekt een steekproef van X1 mensen voor bruin brood, X2 mensen voor wit brood en X3 mensen voor stokbrood. Voor de goede orde: het is trekking zonder teruglegging, dus een persoon kan maar in één van de groepen (1 = bruin brood, 2 = wit brood, 3 = stokbrood) zitten:
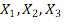
Stel dat je de kwaliteit met een rapportcijfer meet, dan krijg je dus drie gemiddelden:
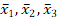
Dit zijn drie onafhankelijk getrokken steekproeven. De gemiddelden beïnvloeden elkaar niet. De steekproefberekening gaat dan per segment:
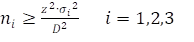
Stel verder dat het steekproefgemiddelde maar een kwart mag afwijken, dat je 95% betrouwbaarheid wil en dat de standaarddeviatie 1,0 bedraagt:
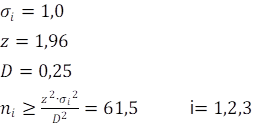
Dus de steekproef per segment is dan 62 personen. Totaal moet je dan 186 verschillende respondenten werven.
Opzet met interactie-effect
Als je nu de opzet wijzigt, zodanig dat elke respondent alle drie soorten broden proeft, dan krijg je te maken met interactie-effecten. Je kunt je dat als volgt voorstellen: stel je hebt een respondent die eerst het ‘ovenheerlijke’ stokbrood proeft, dan het ‘gewone’ witbrood en dan het minder lekkere bruine brood. Deze respondent zal van mening verschillen als de volgorde precies andersom is: eerst het minder lekkere bruine brood, dan het ‘gewone’ witbrood en als laatste het ‘ovenheerlijke’ stokbrood.
De vraag die nu rijst is welke vorm en richting de interactie-effecten hebben. Bijvoorbeeld beïnvloedt X2 de anderen altijd negatief? Of zijn dergelijke veronderstellingen geheel niet voorafgaand aan de meting te maken? Als er geen voorkennis is, dan is het noodzakelijk te veronderstellen dat alle interactie-effecten reëel zijn. De testopzet dient dat te reflecteren door de volgorde waarin de broden geproefd worden telkens te wijzigen. Men krijgt dan per testopzet een segment met bijbehorende steekproeftrekking. Combinatoriek leert dat er n! mogelijke segmenten zijn: voor n=3 zijn dat er dus zes. Zie onderstaande afbeelding.
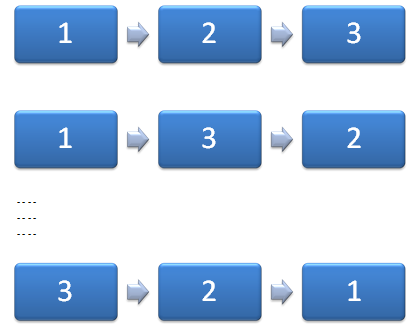
Dat houdt in dat er zes steekproeven getrokken moeten worden. Als dezelfde condities gelden zoals bij de opzet zonder interactie-effect dan geldt ook hier ni=62. Totaal dan 372 verschillende respondenten. Hierbij dient dan wel de voorwaarde gesteld te worden dat de interactie-effecten allemaal onafhankelijk van elkaar zijn, dat is natuurlijk niet helemaal het geval. Het is in dat geval dan ook raadzaam meer respondenten te werven.
Voor de analyse geldt overigens dat de bijbehorende statistiek om de grootte van de interactie-effecten te berekenen is met een full factorial model type III.
Antwoord met Cialdini interactie-effecten
In het geval van de oorspronkelijke vraag met vijf Cialdini-effecten: krijgt elke respondent een Cialdini-effect te zien / te beoordelen? Dan moeten er n! steekproeven getrokken worden en voor n=5 is dat dan 120 steekproeven van elk zeg eens 60 respondenten is dan 7200 respondenten. Dat zou ik niet doen. Ik zou op zoek gaan naar vereenvoudigingen in de onderzoeksopzet,.
- Bijvoorbeeld door te veronderstellen dat de volgorde er niet toe doet. Daarmee verkleint het aantal segmenten tot 10:
- Bijvoorbeeld door elk Cialdini-effect afzonderlijk -zonder die andere effecten in de vragenlijst- uit te vragen. Je maakt dan dus vijf vragenlijsten, per Cialdini-effect één. En trekt dus vijf steekproeven.
Betrouwbaarheid gegeven een steekproefomvang
Vraag van een student
Nu ik respons heb, zie ik dat ik de beoogde 384 respondenten niet heb gehaald. Dat betekent dat ik met minder betrouwbare resultaten genoegen moet nemen. Hoe bereken ik dat?
Antwoord
De steekproefformule voor een metrische variabele herschrijven we dan zodanig dat de betrouwbaarheid ‘eruit’ rolt. Zie onderstaande afleiding (zie p.211).
Om de z-waarde af te leiden, wordt het ongelijkteken een gelijkteken:
Vul de gegevens van de populatie en de steekproef in en voilà je krijgt de z-waarde. Van die z-waarde kun je dan in bijlage III (p.256) de bijbehorende betrouwbaarheid vinden. Stel dat deze gegevens beschikbaar zijn:
In bijlage III vind je dan in de tabel:
Dit is een maximumwaarde. Dus in plaats van 95% betrouwbaarheid, heb je maar 63% betrouwbaarheid. Bedenk dat het opgooien van een geldstuk 50% kans geeft op ‘kop’. Zoveel meer zekerheid biedt dit onderzoek dus niet. Wil je meer zekerheid dat je resultaten te veralgemeniseren zijn naar de populatie toe (extrapolatie), dan moet je je steekproef vergroten.
Likertschaal: ordinaal- of intervalgeschaald
Vraag
Student vroeg mij laatst: mag ik een Likertschaal ook als metrische variabele hanteren?
Antwoord
Hij wist vast niet dat achter die vraag al heel veel literatuur schuilgaat. De essentie is:
- Ja, als je van plan bent een latente variabele te meten. Dus een nieuwe variabele gaat maken op basis van een aantal vragen met een Likertschaal, zoals een attitude.
- Nee, als je alleen maar wil weten wat het antwoord is op een vraag met een Likertschaal.
Daar horen dan ook verschillende analysetechnieken bij (zie hieronder tabel 2). Onderstaand de uitleg van dit antwoord.
Equidistantie
De Likertschaal is een veelgebruikte manier van het vragen naar attitudes en meningen van respondenten (Likert scale, nd). Likert (1932) heeft deze ooit ontworpen om invulling te geven aan de wens om aspecten van persoonlijkheids- en karaktereigenschappen (‘traits of personality and character’) meetbaar te krijgen. De meest gebruikte vorm is in Nederland een vijfpuntsschaal (Brinkman, 2014), maar ook een zevenpuntsschaal komt voor. Een standaard antwoordschaling kent equidistantie ( Likert, 1932; Schriemer, 2014). Equidistantie is een begrip ontleent uit de geografie en betekent ‘gelijke afstanden’. Dat houdt in dit geval in dat de afstand tussen ‘1’ en ‘2’ even groot is als de afstand tussen ‘2’ en ‘3’, enzovoorts. zie tabel 1.
Een voorbeeld waarbij de onderlinge afstanden niet meer gelijk zijn is bijvoorbeeld: 1 = absoluut onwaarschijnlijk, 2 = beetje onwaarschijnlijk, 3 = misschien waarschijnlijk, 4 = waarschijnlijk, 5 = zeer waarschijnlijk. Deze schalen noemen we ongebalanceerd (Berg, Mehciz, Houtkoop-Steenstra & Holleman, 2002) of asymmetrisch (Joshi, Kale, Chandel & Pal, 2012). Over die Likertschaal & -methode is echt veel over geschreven. Een mooi overzichtsartikel is van de hand van Joshi et al (2015) waar ze ingaan op de verschillen en overeenkomsten tussen vijf- en zevenpuntsschalen en (de hamvraag in deze) of je zo’n vraag met een dergelijke schaal nu wel of niet als metrische variabele mag hanteren.
De hamvraag: ordinaal of intervalgeschaald
Om die vraag te beantwoorden moet de onderzoeker eerst vastleggen wat hij wil: een latente variabele meetbaar maken of (losse) vragen stellen die de Likertschaling hebben. Joshi et al (2012) stellen dan ook met klem dat die beslissing vooraf, bij het maken van de vragenlijst, vastgesteld moet zijn door de onderzoeker en dus niet achteraf. Want er is een verschil tussen vragen met de bedoeling een Likertschaal te maken en een Likertschaal-achtige vraag. Boone & Boone (2012) leggen dat omstandig uit.
- “(…) Likert-type items as single questions that use some aspect of the original Likert response alternatives. While multiple questions may be used in a research instrument, there is no attempt by the researcher to combine the responses from the items into a composite scale.”
- “A Likert scale, on the other hand, is composed of a series of four or more Likert-type items that are combined into a single composite score/variable during the data analysis process.”
Het gevolg van die keuze voor de schaling betekent dat er verschillen zijn in de statistische analyses die je kunt uitvoeren. In Schriemer (2017) leg ik uit aan de hand van de tabellen 5.1 (p.132) en 6.1 (p.160) welke analyses gerechtvaardigd zijn, gegeven de schaling van variabelen. In dit specifieke geval omtrent de Likertschalen is de volgende indeling te maken (mede geïnspireerd op de artikelen Boone & Boone (2012) en Joshi et al (2015), zie tabel 2.
Let op: niet neutraal hanteren hè!
Literatuur
Berg, H. van den, Mehciz, M, Houtkoop-Steenstra, H. & Holleman, B. (2002). Opinie-meten of opinie-maken? De rol van stellingvragen in markt- en opinieonderzoek. Amsterdam: Stichting voor Culturele Studies
Boone, H.N. & Boone, D.A. (2012). Analyzing Likert Data. Journal of Extension. Volume 50, No 2, Article number 2TOT2. Geraadpleegd op 03-03-2019 via https://www.researchgate.net/profile/Mahdi_Safarpour/post/what_is_a_logistic_regression_analysis/attachment/59d622fb79197b8077981513/AS:304626539139073@1449640034657/download/Likert+Scale+vs+Likert+Item+%28Good+Source%29.pdf
Brinkman, J.H.M. (2014). De vragenlijst. Een goed meetinstrument voor toepasbaar onderzoek. Groningen/Houten: Noordhoff Uitgevers bv
Joshi, A., Kale, S., Chandel, S. & Pal, D.K. (2015). Likert Scale: Explored and Explained. British Journal of Applied Science & Technology 7(4): 396-403. Geraadpleegd 03-03-2019 via https://www.researchgate.net/publication/276394797_Likert_Scale_Explored_and_Explained
Likert, R. (1932). A technique for the measurement of attitudes. Archives of Psychology, 22(140), pp.1–55.
Likert scale (nd). Likert scale. Geraadpleegd op 12-02-2018 via https://en.wikipedia.org/wiki/Likert_scale
Schriemer, M.G. (20-06-2014). Grrr. Ik ben niet neutraal. [Blog]
Schriemer, M.G. (2017). Statistiek voor de beroepspraktijk. Statistiek leren lezen, daarna begrijpen en berekenen met SPSS. Voor hbo en wo. Tweede herziene druk. Haarlem: SVW
Representativiteit en extrapolatie resultaten
Vraag
Vraag van student: Ik onderzoek of men in Nederland betrokkenheid heeft met het merk X. Ik heb via mijn Facebookpagina respons verzameld en ik zie dat ik nu 51% mannen en 49% vrouwen heb, dat houdt toch in dat ik representatief onderzoek heb gedaan?
Antwoord
Ja, representatief en nee: niet extrapoleren. In de vraag van de student schuilt onbegrip over twee begrippen: representativiteit en extrapoleerbaarheid van de resultaten. Dat laatste houdt in dat de onderzoeksresultaten niet alleen geldig zijn voor de responspopulatie, maar voor de gehele populatie waar de steekproef uit getrokken is.
Voorbeeld
Ik vertaal dit probleem maar even als volgt.
Stel dat ik op het Vrijthof in Maastricht ga staan en ’s middags mensen op het Vrijthof vraag wat zij van de Nederlandse premier vinden. Naast het antwoord (goed / niet goed) noteer ik ook het geslacht van de mensen (man / vrouw / anders). Na vier uur enquêteren heb ik van 733 respondenten respons verzameld; het is een druk plein met het grand café Het Hikkende Heksje in de buurt .
Uit het resultaat blijkt dat de verdeling naar geslacht (man / vrouw) in lijn is met de resultaten van CBS. Dit is met de chikwadraattoets te controleren, dat laat ik nu even aan de lezer over. Zie tabel 1 en 2.
Welke onderzoeksvraag is nu te beantwoorden?
Is de verdeling geslacht man/vrouw representatief met betrekking tot de verhouding in Nederland? Ja
Is dit de mening van ‘de Nederlander’?
Nee: dit is de mening van de bezoeker van het Vrijthof.
Mag je dit resultaat extrapoleren naar ‘Nederland’? Nee. Waarom niet? Stel dat ik op de Grote Markt in Groningen gaan staan (ook een druk plein vanwege het grand café Het Hikkende Heksje in Groningen) en hetzelfde onderzoek herhaal en dan 800 mensen enquêteer. Dan is het zeer denkbaar dat al die mensen een heel ander antwoord geven dan de mensen op het Vrijthof. Om te bewijzen dat het de mening van ‘de Nederlander’ is, zal in heel Nederland geënquêteerd moeten worden.