Levert een Likertschaal een andere meting op dan de semantische differentiaal? Zie blog.
Attitudemeting
Er is een nieuwe blog over het meten van attitudes. Het achterhalen van de waarheid ligt minder voor de hand dan men zou denken.

Zie blog
Gelukkig Nieuwjaar!

Met grote waarschijnlijkheid zijn dit jaar de dagen wederom normaal verdeeld: meer – en minder goede dagen, maar we hopen op een significante uitzondering, meer goede dagen!
Groene bezorging
Sinds kort schakelen wij Fietskoerier Haarlem in voor de boekbezorging.

Zoals zij zelf stellen op hun site: “De groene oplossing voor bezorging in de stad“.
Zij hebben geen last van files, opstoppingen en altijd een parkeerplek voor de deur. Onze boeken worden met zorg in waterdichte tassen geleverd en hun koeriers zijn allen in het bezit van een Verklaring Omtrent Gedrag VOG.
Milieubewust, dus voor een leefbare stad: maatschappelijk verantwoord, geen CO2 uitstoot, zij fietsen zuiver op bruine boterhammen en pasta.
What on earth do communication professionals do?
Eind september 2022 wordt in Wenen tijdens het Euprera congres het artikel gepresenteerd.
Coebergh, P.H., Schriemer, M.G., Cotton, A.M., Blaga, M., Pujol, M.C., Anton, A., Sueldo, M., Gonçalves, G. & Cuenca, J. (2022) What On Earth Do Communication Professionals Do? The anatomy of communication management ( pdf, 419 KB ). Paper to be presented at the EUPRERA 2022 Congress, September 21-24, 2022, Vienna, Austria.
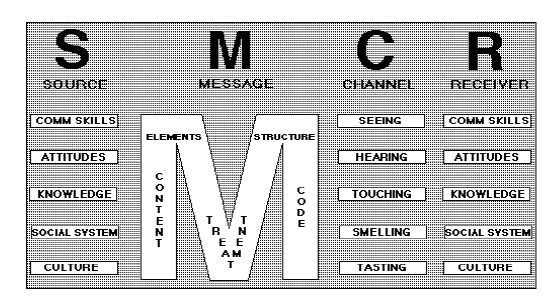
Korte synopsis vind je hier.
As the world gets more connected, the importance of organizational communication rises (Coebergh, 2011; Cornelissen, 2020). However, there is still little agreement on what communication is, let alone how to practice it (Littlejohn et al., 2017). Managing communication is what communication professionals do, for a living. But what do they exactly do, and how should they do it? We started to explore these questions to better understand, and improve, the work of communication professionals, in as many countries we can handle.
Het pdf-document van het gehele artikel vind je hier.
Kruiswoordraadsel
Dit kruiswoordraadsel bevat allerhande begrippen uit onderzoek en statistiek. Veel plezier!
Neemt toeval af en toe toe of af?

Vraag van een student
Neemt de kans op toeval toe of af op het moment dat je steekproefgrootte groter wordt?
Antwoord
Stel je voor dat je lichaamslengte van mensen meet. Van CBS weten we dat gemiddelde lengte van de man ca. 1,84 meter is.
CBS: https://www.cbs.nl/nl-nl/nieuws/2021/37/nederlanders-korter-maar-nog-steeds-lang
Stel nu het volgende voor: je trekt een steekproef van 20 mensen uit het GBA (=Gemeentelijke Basis Administratie) van Utrecht. En je meet van die mensen de gemiddelde lengte, dat blijkt 2,02 meter te zijn.

“Wat is hier aan de hand?” denk je dan.
Controle van de steekproef geeft dat je heel toevallig allemaal mannen van de basketbalvereniging in je steekproef hebt. Dus als je je steekproef nu vergroot naar 350.000 mensen (ca. alle mensen in Utrecht) dan kom je wél uit op 1,84 meter gemiddeld.
Wikipedia (2021): https://nl.wikipedia.org/wiki/Utrecht_(stad)
Voorbeeld met leeftijden
Stel je trekt een steekproef met totaal 15 respondenten. Je berekent na elke trekking van een respondent steeds het nieuwe gemiddelde. Dus het gemiddelde over 3 respondenten is dan (24+12+66)/3=34.
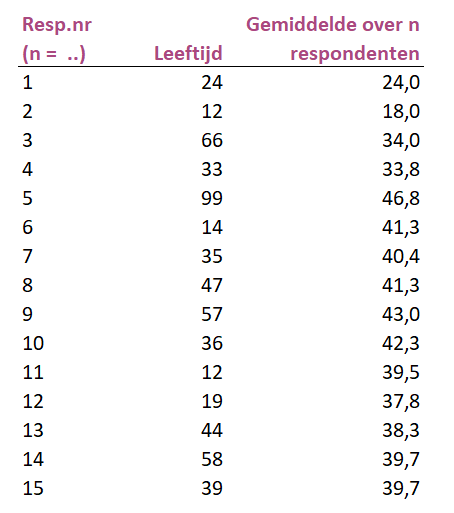
Dat toeval afneemt en dus het werkelijke populatiegemiddelde benadert laat onderstaande grafiek zien op basis van bovenstaande gegevens van de tabel. De wijnrode lijn geeft de leeftijd van de respondent weer. De zwarte lijn het berekende gemiddelde over n respondenten.
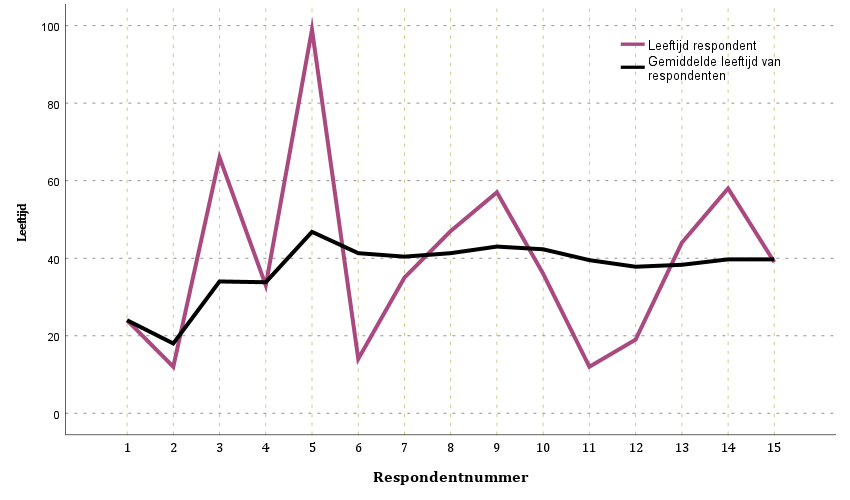
Duidelijk is dat de gemiddelde leeftijd al snel (na respondent 5) rondom de veertig jaar schommelt, terwijl respondenten wisselende leeftijden hebben.
Conclusie
Het kan zijn dat als je de steekproef stapsgewijs vergroot, dat de toeval eerst toeneemt en dan afneemt, omdat het gemiddelde erg kan schommelen. Maar in het algemeen geldt dat …
Toeval neemt af naarmate de steekproef groter wordt.
Wordt standaarddeviatie kleiner?

Vraag van een student
Wordt de standaarddeviatie per se kleiner als je meer mensen aan je steekproef toevoegt?
Antwoord
Als je een voorbeeld vindt dat het tegenovergestelde bewijst, dan weet je dat die ‘regel’ niet opgaat.
Stel je voor dat je van vijf mensen hebt gevraagd wat hun leeftijd is: 23, 24, 25, 26, 27. Gemiddelde is 25 jaar, de standaarddeviate = 1,6. Stel dat je nu je steekproef vergroot met nog eens vijf mensen uit de populatie en die hebben de leeftijden: 55, 101, 12, 98, 15. Dan is het gemiddelde 40,6 jaar met standaarddeviatie 33,1.
Dus, nee. De standaarddeviatie wordt niet perse kleiner als je meer mensen aan je steekproef toevoegt.
Heel soms is statistiek ook niet alles
“Dromen en angsten overtreffen statistiek”
Piet Hein Coebergh (2020)
Bron: Coebergh, P.H.C. (2020). Big brother. Adformatie Vol 2, februari 2020.

Galton bord
Zoals in hoofdstuk 4 is uiteengezet, visualiseert een Galton bord het ontstaan van de normale verdeling.
Klik voor de animatie.
