Je hebt niet meer kans met waarschijnlijkheidsrekening, maar je komt tot een beter besluit.

Je hebt niet meer kans met waarschijnlijkheidsrekening, maar je komt tot een beter besluit.

Statistische toetsen lijkt op schaken. Hoe meer vrijheden (voor de koning), des te ingewikkelder de berekening (het mat zetten).

In het algemeen kan men stellen dat een statistische toets gecorrigeerd moet worden voor onnauwkeurigheden, daardoor verlies je een of meerdere graden van vrijheid.
Het werken met steekproefgemiddelden, in plaats van populatie gemiddelden levert onnauwkeurigheden op, die in (bijv.) de t-toets worden gecorrigeerd met een aantal graden van vrijheid.
In de literatuur: Graden van vrijheid = gvv. Angelsaksische literatuur: Degrees of freedom = df.
Geen mooiere verzameling denkbaar dan een database.
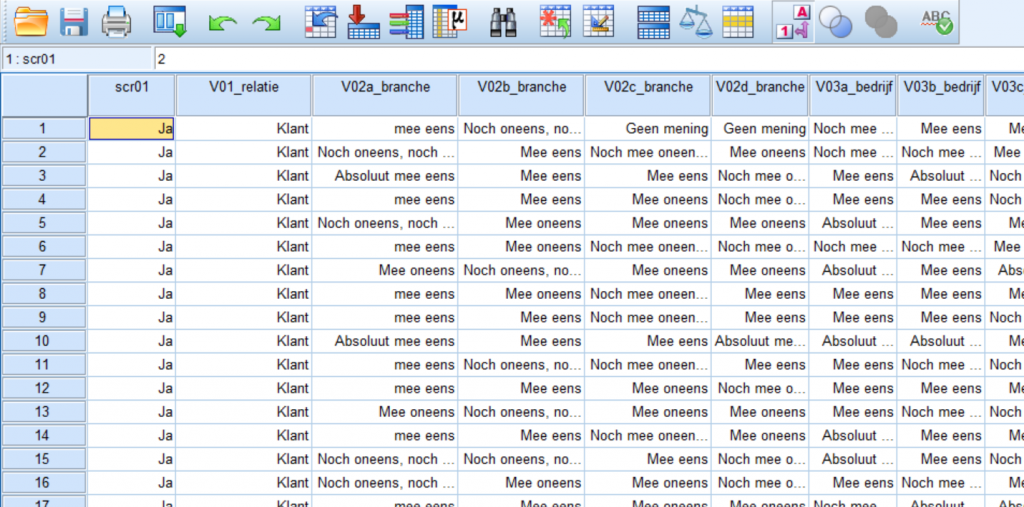
Een database is eigenlijk niets anders dan een elektronische tabel.
Maar daar bedoelen we niet mee dat een scheve verdeling ook een ‘normale verdeling’ is!
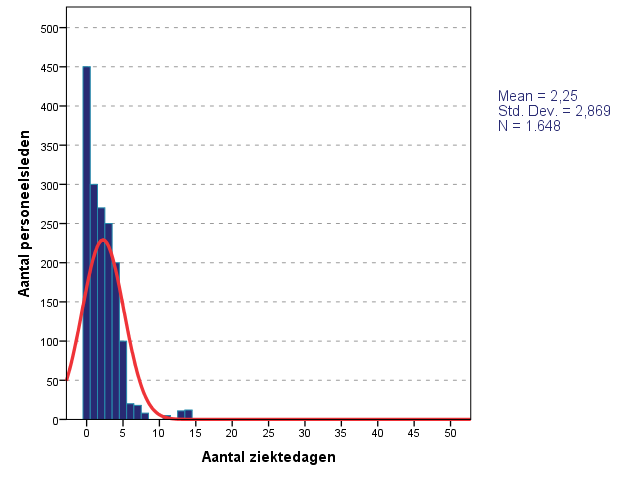
HRM-afdelingen houden bij hoe vaak een werknemer ziek is. Het is normaal dat men niet ziek is, nou ja, soms een verkoudheid of zo. Dus elke werknemer heeft meestal minder dan vijf ziektedagen.
Dus hier een scheve verdeling met de staart naar rechts.
De verdeling is scheef, want een paar werknemers trekken het gemiddelde omhoog. Daarom is het bij scheve verdelingen vaak beter de mediaan te hanteren.
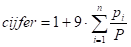
Dit is de formule voor je tentamencijfer. De 1 krijg je gratis. Met p(i) is bedoeld het aantal behaalde punten per vraag, P is het maximum aantal te behalen punten en er zijn totaal n vragen.
Stel er zijn 40 vragen,1 punt per vraag en je hebt 23 goed, dan heb je een 6,2.
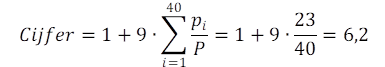


Ook wel student t-toets genoemd. Zie voor beschrijving William Sealy Gosset bijv. wikipedia
T-toets is een veelvuldig hulpmiddel, bijvoorbeeld bij het vergelijken van twee steekproefgemiddelden, of om een steekproefgemiddelde te vergelijken met een bepaald getal (zoals het populatiegemiddelde), zie onderstaande formule.
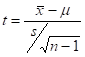
Student: ‘een lege verzameling is niet te controleren, want hoe zie je niets?’

Nou ja, we zien wel ‘niets’. We tellen immers het aantal elementen. Als je het aantal aardappelen in de pan telt en je telt nul aardappelen, dan is de verzameling aardappelen in de pan ‘leeg’.

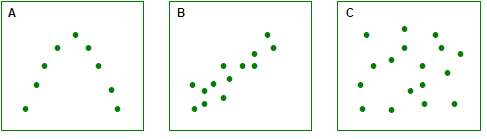
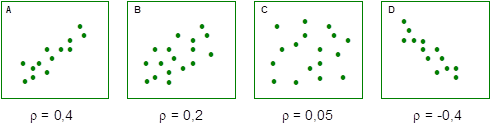
Zorgvuldigheid geboden bij het beoordelen van de correlatiecoëfficiënt.
Don’t be rash!