Dit kruiswoordraadsel bevat allerhande begrippen uit onderzoek en statistiek. Veel plezier!
Categorie: Statistiek
Neemt toeval af en toe toe of af?
Vraag van een student
Neemt de kans op toeval toe of af op het moment dat je steekproefgrootte groter wordt?
Antwoord
Stel je voor dat je lichaamslengte van mensen meet. Van CBS weten we dat gemiddelde lengte van de man ca. 1,84 meter is.
CBS: https://www.cbs.nl/nl-nl/nieuws/2021/37/nederlanders-korter-maar-nog-steeds-lang
Stel nu het volgende voor: je trekt een steekproef van 20 mensen uit het GBA (=Gemeentelijke Basis Administratie) van Utrecht. En je meet van die mensen de gemiddelde lengte, dat blijkt 2,02 meter te zijn.
“Wat is hier aan de hand?” denk je dan.
Controle van de steekproef geeft dat je heel toevallig allemaal mannen van de basketbalvereniging in je steekproef hebt. Dus als je je steekproef nu vergroot naar 350.000 mensen (ca. alle mensen in Utrecht) dan kom je wél uit op 1,84 meter gemiddeld.
Wikipedia (2021): https://nl.wikipedia.org/wiki/Utrecht_(stad)
Voorbeeld met leeftijden
Stel je trekt een steekproef met totaal 15 respondenten. Je berekent na elke trekking van een respondent steeds het nieuwe gemiddelde. Dus het gemiddelde over 3 respondenten is dan (24+12+66)/3=34.
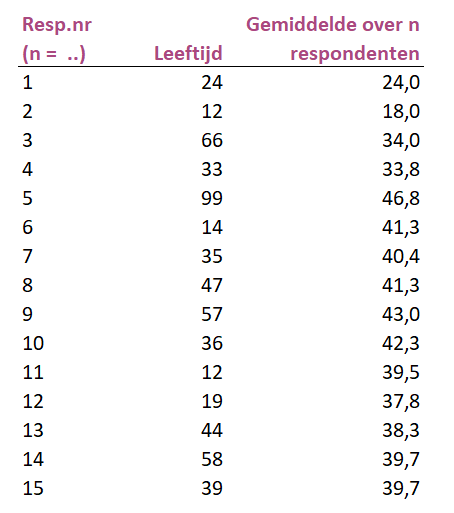
Dat toeval afneemt en dus het werkelijke populatiegemiddelde benadert laat onderstaande grafiek zien op basis van bovenstaande gegevens van de tabel. De wijnrode lijn geeft de leeftijd van de respondent weer. De zwarte lijn het berekende gemiddelde over n respondenten.
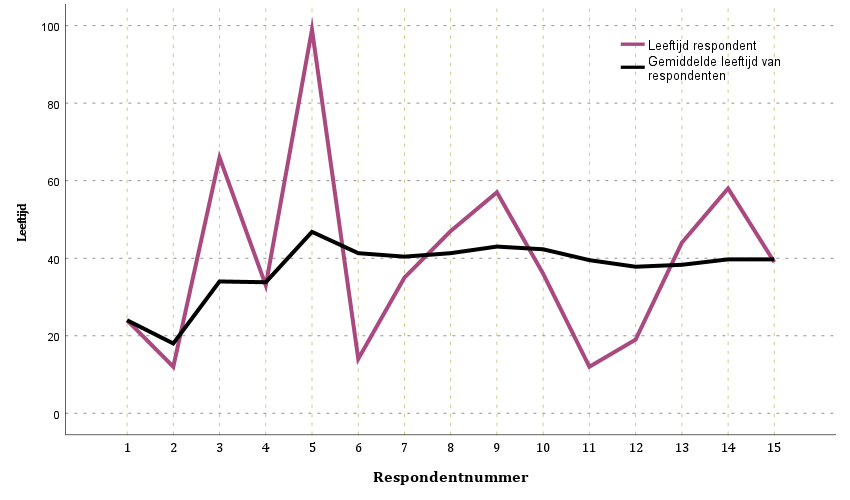
Duidelijk is dat de gemiddelde leeftijd al snel (na respondent 5) rondom de veertig jaar schommelt, terwijl respondenten wisselende leeftijden hebben.
Conclusie
Het kan zijn dat als je de steekproef stapsgewijs vergroot, dat de toeval eerst toeneemt en dan afneemt, omdat het gemiddelde erg kan schommelen. Maar in het algemeen geldt dat …
Toeval neemt af naarmate de steekproef groter wordt.
Wordt standaarddeviatie kleiner?
Vraag van een student
Wordt de standaarddeviatie per se kleiner als je meer mensen aan je steekproef toevoegt?
Antwoord
Als je een voorbeeld vindt dat het tegenovergestelde bewijst, dan weet je dat die ‘regel’ niet opgaat.
Stel je voor dat je van vijf mensen hebt gevraagd wat hun leeftijd is: 23, 24, 25, 26, 27. Gemiddelde is 25 jaar, de standaarddeviate = 1,6. Stel dat je nu je steekproef vergroot met nog eens vijf mensen uit de populatie en die hebben de leeftijden: 55, 101, 12, 98, 15. Dan is het gemiddelde 40,6 jaar met standaarddeviatie 33,1.
Dus, nee. De standaarddeviatie wordt niet perse kleiner als je meer mensen aan je steekproef toevoegt.
Galton bord
Zoals in hoofdstuk 4 is uiteengezet, visualiseert een Galton bord het ontstaan van de normale verdeling.
Klik voor de animatie.
Drie wensen
De onderzoeker rommelde wat in een oude, reeds lang verlaten schuur en vond tot zijn verbazing een koperen lamp. Hij veegde het stof eraf en tot zijn verbazing verscheen er een geest. “Je mag drie wensen doen” zei de geest tot de verbaasde onderzoeker. De onderzoeker wist het wel. Hij rende terug naar huis, de geest achter hem aan zwevend, nam plaats achter zijn laptop en sprak vervolgens zijn drie wensen uit …
1e wens: representatief onderzoek
De onderzoeker stamelde wat onduidelijks, maar hij hervond zich al snel en zei “ik wens representatief onderzoek!”
“Uw wens is vervuld” zei de geest.
De onderzoeker analyseerde snel zijn data met behulp van SPSS en zag dat de clustersteekproeven op correcte wijze aselect waren uitgevoerd. Hij analyseerde de respons met de chikwadraattoets om te bezien of de leeftijden en het geslacht van de respondenten representatief waren ten opzichte van de populatie. De gegevens van CBS erbij gehaald en opgenomen in de chikwadraattoetsing. En ja hoor! Allemaal p-waarden boven de 5%!
Tevreden leunde hij achterover.
2e wens: valide onderzoek
Nu dit voor elkaar was, wreef hij weer over de lamp en de geest, onvermoeibaar, verscheen weer voor hem. De onderzoeker wenste resoluut “ik wens valide onderzoek!”
“Uw wens is vervuld” zei de geest.
De onderzoeker keek naar zijn vragenlijst en deze was op slag veranderd. Alle begrippen waar respondenten over konden struikelen waren allemaal aangepast. De volgorde van de vragenlijst was aangepast, alle matrixvraagblokken waren voorzien van een introductie, moeilijke begrippen stonden in een extra toelichting netjes uiteengezet. Ook de antwoordopties waren aangepast. Nette, equidistante Likertschalen, afgewisseld met semantische differentialen, half-open vragen en dichotomieën. En natuurlijk was als allerlaatste vraag toegevoegd “Heeft u vragen, opmerkingen of suggesties? We vernemen het graag.”
Tevreden leunde hij achterover.
3e wens: betrouwbaar onderzoek
Glimlachend keek hij naar de lamp en wreef er voor de derde keer erover. De geest verscheen en sprak hem toe “U heeft nog één wens, wat wenst u?”
Ook nu was de onderzoeker stellig “ik wens betrouwbaar onderzoek!”
“Uw laatste wens is vervuld” zei de geest.
De onderzoeker keek weer naar zijn data en zag dat elke analyse die hij deed meer dan 95% betrouwbaarheid in zich had. De pearsoncorrelatiecoëfficiënten waren allemaal met meer dan 95% betrouwbaarheid afwijkend van nul. Zijn t-toetsen om de gemiddelden te vergelijken gaven allemaal meer dan 95% betrouwbaarheid over het toetsresultaat. Ook zijn regressiecoëfficiënten gaven een betrouwbaar toetsresultaat.
Tevreden leunde hij achterover.
Eindrapportage
Tevreden met zichzelf presenteerde hij de resultaten aan zijn opdrachtgever. Hij ging zo op in zijn zelfgenoegzaamheid, dat hij niet merkte dat de wenkbrauwen van de opdrachtgever hoger en hoger van verbazing opgetrokken waren. Nog voordat hij klaar was met zijn presentatie kon de opdrachtgever zich niet meer inhouden en sprong op, gooide daarmee zijn stoel omver en riep uit “Dit onderzoek is niet bruikbaar!”
Gedesillusioneerd zat de onderzoeker weer achter zijn bureau en wreef de lamp tot glanzend koper in het zonlicht, maar zijn drie wensen waren verbruikt.
Kerstbalongeluk
Vraag van student: “In mijn leven heb ik tot op heden twee kerstballen laten vallen, ik ben nu 20 jaar. Hoe groot is de kans dat ik vier keer een kerstbal laat vallen?”
Antwoord
Voor dergelijke kansverdelingen is er de Poisson-verdeling. Een verdeling voor zeldzame gebeurtenissen. De formule voor de kansverdeling:
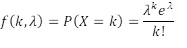
We veronderstellen in dit voorbeeld van de student dat die twee keer een goede verwachting is van het aantal keer dat zij een kerstbal laat vallen. Dan wordt:
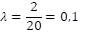
De kans dat deze student de bal bijvoorbeeld vier keer laat vallen is dan:
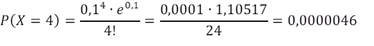
Oftewel ongeveer 1 op de 250.000.
Voor verdere informatie zie bijvoorbeeld:
- Rijken van Olst, H. (1974). Algemene statistiek. Een moderne inleiding tot de statistische theorie. Assen: Van Gorcum & Comp. B.V.
- https://en.wikipedia.org/wiki/Poisson_distribution
Kleinstekwadratenmethode
Uitleg over de kleinstekwadratenmethode, zie clip https://youtu.be/Y6sfXrhnYbI
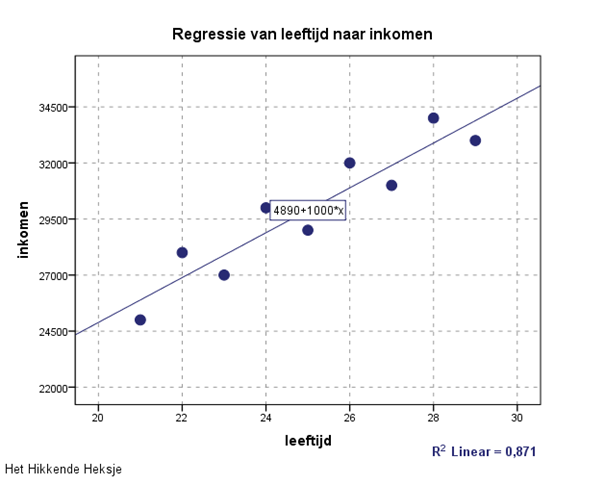
Uitleg over (het ontstaan van) de kleinstekwadratenmethode van Carl Friedrich Gauss en het bewijs dat er maar één oplossing is voor de lijn door de puntenwolk met het minste residu.
Multiresponsanalyses
In plaats van vele frequentietabellen van dichotome variabelen beantwoord je in een keer met SPSS de volgende onderzoeksvragen:
- Welk onderdeel/vraag/item is het meest aangekruist?
- Welk onderdeel/vraag/item is het minst aangekruist?
- Hoeveel onderdelen/vragen/items zijn gemiddeld aangekruist?
Zie clip multiresponsanalyse
Mediaan & spreiding
De boxplot visualiseert de relatie tussen de mediaan en de spreiding.
De spreiding is weergegeven via kwartielen, minimum en maximum.
Somer, niet zomer hè
Voor het toetsen van asymmetrische ordinale relaties hanteer je Somers’ d.
Nee, niet ‘summer‘ …
