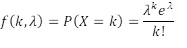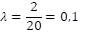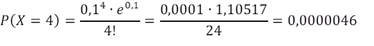Kansen – Het Hikkende Heksje

Neemt toeval af en toe toe of af?

Vraag van een student

Neemt de kans op toeval toe of af op het moment dat je steekproefgrootte groter wordt?

Antwoord

Stel je voor dat je lichaamslengte van mensen meet. Van CBS weten we dat gemiddelde lengte van de man ca. 1,84 meter is.

CBS: https://www.cbs.nl/nl-nl/nieuws/2021/37/nederlanders-korter-maar-nog-steeds-lang

Stel nu het volgende voor: je trekt een steekproef van 20 mensen uit het GBA (=Gemeentelijke Basis Administratie) van Utrecht. En je meet van die mensen de gemiddelde lengte, dat blijkt 2,02 meter te zijn.

“Wat is hier aan de hand?” denk je dan.

Controle van de steekproef geeft dat je heel toevallig allemaal mannen van de basketbalvereniging in je steekproef hebt. Dus als je je steekproef nu vergroot naar 350.000 mensen (ca. alle mensen in Utrecht) dan kom je wél uit op 1,84 meter gemiddeld.

Wikipedia (2021): https://nl.wikipedia.org/wiki/Utrecht_(stad)

Voorbeeld met leeftijden

Stel je trekt een steekproef met totaal 15 respondenten. Je berekent na elke trekking van een respondent steeds het nieuwe gemiddelde. Dus het gemiddelde over 3 respondenten is dan (24+12+66)/3=34.

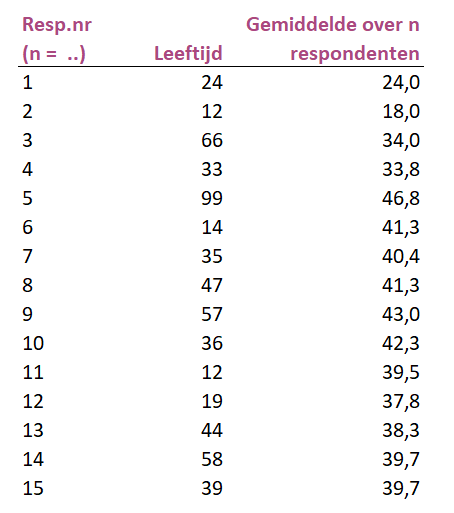
Dat toeval afneemt en dus het werkelijke populatiegemiddelde benadert laat onderstaande grafiek zien op basis van bovenstaande gegevens van de tabel. De wijnrode lijn geeft de leeftijd van de respondent weer. De zwarte lijn het berekende gemiddelde over n respondenten.

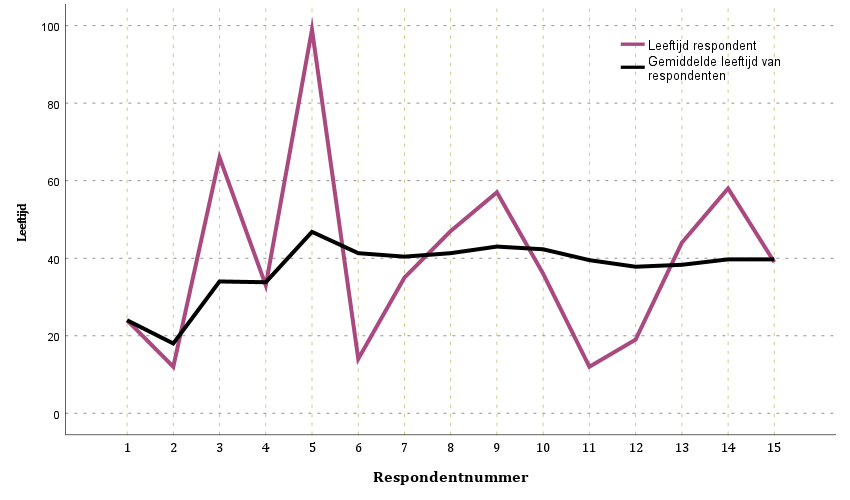
Grafische weergave van de schommelende *gemiddelde leeftijd*.

Duidelijk is dat de gemiddelde leeftijd al snel (na respondent 5) rondom de veertig jaar schommelt, terwijl respondenten wisselende leeftijden hebben.

Conclusie

Het kan zijn dat als je de steekproef stapsgewijs vergroot, dat de toeval eerst toeneemt en dan afneemt, omdat het gemiddelde erg kan schommelen. Maar in het algemeen geldt dat …

Toeval neemt af naarmate de steekproef groter wordt.

Kerstbalongeluk

Vraag van student: “In mijn leven heb ik tot op heden twee kerstballen laten vallen, ik ben nu 20 jaar. Hoe groot is de kans dat ik vier keer een kerstbal laat vallen?”

Antwoord

Voor dergelijke kansverdelingen is er de Poisson-verdeling. Een verdeling voor zeldzame gebeurtenissen. De formule voor de kansverdeling:

We veronderstellen in dit voorbeeld van de student dat die twee keer een goede verwachting is van het aantal keer dat zij een kerstbal laat vallen. Dan wordt:

De kans dat deze student de bal bijvoorbeeld vier keer laat vallen is dan:

Oftewel ongeveer 1 op de 250.000.

Voor verdere informatie zie bijvoorbeeld:

Rijken van Olst, H. (1974). Algemene statistiek. Een moderne inleiding tot de statistische theorie. Assen: Van Gorcum & Comp. B.V.
https://en.wikipedia.org/wiki/Poisson_distribution

Meer kans?

Je hebt niet meer kans met waarschijnlijkheidsrekening, maar je komt tot een beter besluit.

Photo (edited) by Mert Kahveci on Unsplash

Verkeerde handen

Deze student heeft het begrip kansen nog niet helemaal door: ‘als de kansen in verkeerde handen vallen, ben je de sjaak!’

Randomisatie

Student zegt vertwijfeld: ‘bij randomisatie krijg je elke keer weer iets anders!’

Kansen draaien om verwachtingen.

Dus niet: kansen draaien óm bij verwachtingen.

Uniforme verdeling

De uniforme verdeling komt vaker voor dan je denkt.

Alles is toeval

Zuivere politici?

Tijdens college over kansen: ‘als een dobbelsteen zuiver is, dan is de geometrie van de kubus conform de fysische eigenschappen gelijkelijk verdeeld’ repliceert de student ‘hoe zouden we zuiverheid van veelzijdige politici kunnen meten met waarschijnlijkheidsrekening?’

Gehaald of gezakt?

Student verzucht naar vriend: ‘wat is de kans dat ik het tentamen in één keer haal’?

Vriend: ‘Dûh … 50%, je haalt het of niet’.