Vraag van student: “In mijn leven heb ik tot op heden twee kerstballen laten vallen, ik ben nu 20 jaar. Hoe groot is de kans dat ik vier keer een kerstbal laat vallen?”

Antwoord
Voor dergelijke kansverdelingen is er de Poisson-verdeling. Een verdeling voor zeldzame gebeurtenissen. De formule voor de kansverdeling:
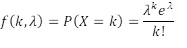
We veronderstellen in dit voorbeeld van de student dat die twee keer een goede verwachting is van het aantal keer dat zij een kerstbal laat vallen. Dan wordt:
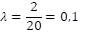
De kans dat deze student de bal bijvoorbeeld vier keer laat vallen is dan:
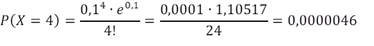
Oftewel ongeveer 1 op de 250.000.
Voor verdere informatie zie bijvoorbeeld:
- Rijken van Olst, H. (1974). Algemene statistiek. Een moderne inleiding tot de statistische theorie. Assen: Van Gorcum & Comp. B.V.
- https://en.wikipedia.org/wiki/Poisson_distribution
